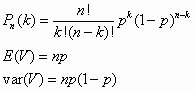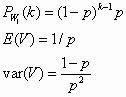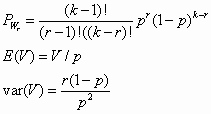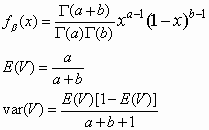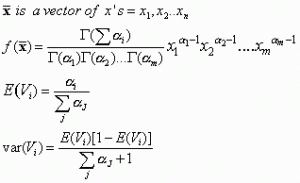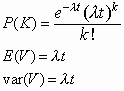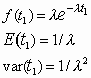BINOMIAL

A two outcome experiment (coin toss) with

• probability p to have S
• probability 1-p to have F

is repeated n times and the number of times (k) that S comes up and the number of times (n-k) that F comes up.

The order is not retained.

P_n(k) is the prob of k S values.

Each trial is independent of past trials.

GEOMETRIC

A ‘coin’ is tossed until a head (S) shows. The tosses are independent.

Pw1(k) is the waiting time (number of trials) needed to reach the first head, where p is the prob of S, k is the trial where the first success occurs.

PASCAL

Is the waiting time (number of trials) needed to reach the r^th S value in a two outcome experiment where each trial is independent of previous trials.

P is the prob of S in each trial. K is the trial number when the r^th S occurs.

BETA DENSITY

If a two outcome experiment has

• a-1 values of S
• b-1 values of F

What is the value of p? The random variable gives the interval probability for possible p values.

Multinomial Density

Similar to binomial density except m possible outcomes on each independent trial (consider a 6 sided die and question what is the prob of 3 ones, 2 fives, 0 sixes, 1 two in 6 rolls of the die.

Dirichlet Density

Similar to Beta

Despite the heavy use of Greek letters and impossible to compute by hand. This is easy to use! The computer does the final integral equation. Most of the use can be done by hand on the back of an envelope.

Gaussian (Normal) Density

When all else fails... 

Poisson

Another work horse—also a limit

t is the time interval to be examined

λ is the rate of ‘events’ per unit time

k is the number of events which occurred

Exponential Density

Is the waiting time to the first event of a Poisson process

i.e., given l, how long is the wait until the first event.

Gamma (Erlanger) Density

The wait time until the r^th event of a Poisson Process with rate l.