(4). Opportunities and loose ends
(i). Changes and causes [CONTENT to be added]
(ii). Spatial analyses
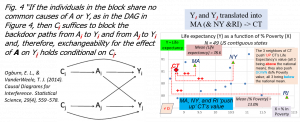
***Analyzing spatial (or areal, regional) data adds more statistical and causal challenges. The mere ‘average’ (or E, expectation) value of a variable, say the mean (across all county residents) county life expectancy across all the US counties cannot be computed simply with the arithmetic average. The reason can be ‘seen’ if one considers a roulette, or horizontal ‘wheel of fortune’, where the numbers are ordered consecutively, 1,2,3, etc. If a ‘fair’ roulette is jimmied or altered, by adding a weight underneath to tilt the wheel slightly, the number above the added weight will be favored: the probabilities of getting each number are not equal anymore[i], but they are related: the numbers next to this ‘luckiest’ number have 2nd highest probabilities, 3rd highest, and so on, walking away from it. This same type of neighboring-similarity is what makes spatial data more complex: the formulas for the average, for the conditional average, and for the size of the effect of predictors need to be adjusted; one demonstration is here FamilyPractice, and a demo here Tinyurl.com/BLOGSTATS3 (Youtube @ Tinyurl.com/INTRSTATS3 but there is also a ‘hands on’ Excel workbook showing how and why things differ, using the 49 contiguous US states as example @ Tinyurl.com/SPATIALSSM ). Briefly, say CT’s (average, across all residents) Life Expectancy (LifeExpectancy.CT) is impacted by its neighbors’ values, (see Figure):
LifeExpectancyMA & NY & RI -> LifeExpectancyCT; similarly,
%PovertyMA & NY & RI -> %PovertyCT;
and this is even before trying to find the Effect.%Poverty -> LifeExpectancy!
(ii). New/modern emerging statistical tools: and NO! I have not read these, neither do I follow these publications regularly, someone else does, however: Cam Mcintosh, who shares his knowledge on SEMNET.
- Revolutionary: Carlos Cinelli’s Pearl vs. ‘Rubin’ (SCM-RCM) equivalence demonstration Semnet 1 and Semnet 2
- The E value [2, 3] – with R code
- Fair inference: ‘some covariates or treatments are “sensitive,” in the sense of having potential of creating discrimination’ [4, 5]; Elias Bareinboim [5]
- Graphical Hierarchy of Interventions: see Shpister & Tchetgen [6]
- Personalized Individual effects [7] [8] & [9] + [10] [11] [12] [13] [14] [15]
- Attrition/missingness [16]
- Interventional effects [17] standardized expectations of potential outcomes
- Planned precision vs. planned power [18]
- Evidence strength for causality [3]
- Single world interventions [19]
- Mediation Analysis with Attributable Fractions [20]– with R code
- LiNGAM [21-27] + 12.1 Bayesian estimation of causal direction in acyclic structural equation models [28]
- Information Geometric Causal Inference Criterion (IGCIC) [29, 30] &Applied: Gaussian process model and ICCIC [31]
- Causal Generative Neural Networks (CGNN) [32]
- Multivariate additive noise model (MANM) [33]
- Causal inference on discrete data via estimating distance correlations [34]
- Causal Inference by Stochastic Complexity [35] & [36]
- Nonparametric Quantile-Based Causal Discovery
- Direction of dependence [37] [38] [39] [40]; Cam McIntosh SEMNET
- Direction Dependence Analysis
- Higher order moments (skew) to derive directionality ; e.g. in mediation [41]
- Population Health Model (POHEM) [42], & Micro-simulation [43], & DAG-informed regression modelling [44]
- Lag as moderator for synthesizing longitudinal data [45]
- More of Cam McIntosh SEMNET or TXT
- More of Cam Nonparametric Simultaneous Equations e.g.
- In other fields: physics [46]; paleontology [47];
- In relation to chaos/nonlinear dynamical systems[48-55] ;
- Microrandomized trials [56, 57] and Contextual Bandit Algorithm [58, 59]
- Power priors [60-71]
- Convergent cross mapping [72]
- Bayesian networks applied in medicine [73] & [74-91]
- Dynamical systems analyses www
*** This concludes the 4 step walk-through in the ‘research methods’/statistics introduction centered on causality. There is of course much more to cover/investigate, but in this age of AI, every one of us tends to become an equally good teacher’, with proper questioning and nuanced interpreting of AI’s response.
References
- Stigler, S.M., The history of statistics: The measurement of uncertainty before 1900. 1986: Harvard University Press.
- VanderWeele, T.J. and P. Ding, Sensitivity analysis in observational research: introducing the E-value. Annals of internal medicine, 2017. 167(4): p. 268-274.
- Mathur, M.B., et al., Web Site and R Package for Computing E-values. Epidemiology, 2018. 29(5): p. e45-e47.
- Nabi, R. and I. Shpitser, Fair inference on outcomes, in Proceedings of the AAAI Conference on Artificial Intelligence. 2018, NIH Public Access. p. 1931.
- Zhang, J. and E. Bareinboim, Fairness in Decision-Making–The Causal Explanation Formula, in 32nd AAAI Conference on Artificial Intelligence. http://causalai.net/r30.pdf. 2018.
- Shpitser, I. and E.T. Tchetgen, Causal inference with a graphical hierarchy of interventions. Annals of statistics, 2016. 44(6): p. 2433.
- Shpitser, I. and E. Sherman. Identification of Personalized Effects Associated With Causal Pathways. in proceedings of the 34th Conference on Uncertainty in Artificial Intelligence. 2018.
- Nabi, R., P. Kanki, and I. Shpitser. Estimation of Personalized Effects Associated With Causal Pathways. in Proceedings of the Thirty Fourth Conference on Uncertainty in Artificial Intelligence (UAI). 2018.
- Shpitser, I. and S. Sarkar, Personalizing Path-Specific Effects. arXiv preprint arXiv:1709.03862, 2017.
- Zhang, Y., A. Bellot, and M. van der Schaar, Learning overlapping representations for the estimation of individualized treatment effects https://arxiv.org/pdf/2001.04754.pdf. 2020.
- Henderson, N.C., et al., Individualized treatment effects with censored data via fully nonparametric Bayesian accelerated failure time models. Biostatistics, 2020. 21(1): p. 50-68.
- Lamont, A., et al., Identification of predicted individual treatment effects in randomized clinical trials. Statistical methods in medical research, 2018. 27(1): p. 142-157.
- Zhao, Y.-Q., M.W. Redman, and M.L. LeBlanc, Quantifying treatment effects using the personalized chance of longer survival. Statistics in Medicine, 2019. 38(28): p. 5317-5331.
- Anoke, S.C., S.L. Normand, and C.M. Zigler, Approaches to treatment effect heterogeneity in the presence of confounding. Statistics in medicine, 2019. 38(15): p. 2797-2815.
- Cui, Y. and E. Tchetgen Tchetgen, A semiparametric instrumental variable approach to optimal treatment regimes under endogeneity. Journal of the American Statistical Association, 2020: p. 1-12.
- Cinelli, C. and J. Pearl, On the utility of causal diagrams in modeling attrition: a practical example. 2018.
- Moreno-Betancur, M. and J.B. Carlin, Understanding Interventional Effects: A More Natural Approach to Mediation Analysis? Epidemiology, 2018. 29(5): p. 614-617.
- Rothman, K.J. and S. Greenland, Planning Study Size Based on Precision Rather Than Power. Epidemiology, 2018. 29(5): p. 599-603.
- Breskin, A., S.R. Cole, and M.G. Hudgens, A practical example demonstrating the utility of single-world intervention graphs. Epidemiology, 2018. 29(3): p. e20-e21.
- Sjölander, A., Mediation Analysis with Attributable Fractions. Epidemiologic Methods, 2018.
- Hoyer, P.O., et al., Causal discovery of linear acyclic models with arbitrary distributions. arXiv preprint arXiv:1206.3260, 2012.
- Hoyer, P.O., et al., Estimation of causal effects using linear non-Gaussian causal models with hidden variables. International Journal of Approximate Reasoning, 2008. 49(2): p. 362-378.
- Shimizu, S., LiNGAM: Non-Gaussian methods for estimating causal structures. Behaviormetrika, 2014. 41(1): p. 65-98.
- Shimizu, S., Non-Gaussian structural equation models for causal discovery, in Statistics and Causality: Methods for Applied Empirical Research, K. Zhang and A. Hyvärinen, Editors. 2016. p. 153-184.
- Shimizu, S., et al., A linear non-Gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 2006. 7(Oct): p. 2003-2030.
- Shimizu, S., et al., DirectLiNGAM: A direct method for learning a linear non-Gaussian structural equation model. Journal of Machine Learning Research, 2011. 12(Apr): p. 1225-1248.
- Shimizu, S. and Y. Kano, Use of non-normality in structural equation modeling: Application to direction of causation. Journal of Statistical Planning and Inference, 2008. 138(11): p. 3483-3491.
- Shimizu, S. and K. Bollen, Bayesian estimation of causal direction in acyclic structural equation models with individual-specific confounder variables and non-Gaussian distributions. Journal of Machine Learning Research, 2014. 15(1): p. 2629-2652.
- Janzing, D., et al., Information-geometric approach to inferring causal directions. Artificial Intelligence, 2012. 182-183: p. 1-31.
- Janzing, D., et al., Justifying information-geometric causal inference, in Measures of Complexity. 2015, Springer. p. 253-265.
- Zhang, Y., Y. Cen, and G. Luo, Causal direction inference for air pollutants data. Computers & Electrical Engineering, 2018. 68: p. 404-411.
- Goudet, O., et al., Learning functional causal models with generative neural networks, in Explainable and Interpretable Models in Computer Vision and Machine Learning https://arxiv.org/pdf/1709.05321.pdf. 2018, Springer. p. 39-80.
- Parida, P.K., T. Marwala, and S. Chakraverty, A multivariate additive noise model for complete causal discovery. Neural Networks, 2018. 103: p. 44-54.
- Liu, F. and L. Chan, Causal inference on discrete data via estimating distance correlations. Neural computation, 2016. 28(5): p. 801-814.
- Budhathoki, K. and J. Vreeken, Causal Inference by Stochastic Complexity. arXiv preprint arXiv:1702.06776, 2017.
- Kocaoglu, M., et al. Entropic Causal Inference. in AAAI. 2017.
- Dodge, Y. and I. Yadegari, On direction of dependence. Metrika, 2010. 72(1): p. 139-150.
- Dodge, Y. and V. Rousson, Direction dependence in a regression line. Communications in Statistics-Theory and Methods, 2000. 29(9-10): p. 1957-1972.
- Muddapur, M., On directional dependence in a regression line. Communications in Statistics-Theory and Methods, 2003. 32(10): p. 2053-2057.
- Sungur, E.A., A note on directional dependence in regression setting. Communications in Statistics—Theory and Methods, 2005. 34(9-10): p. 1957-1965.
- Wiedermann, W., X. Li, and A. von Eye, Testing the Causal Direction of Mediation Effects in Randomized Intervention Studies. Prevention Science, 2018.
- Hennessy, D.A., et al., The Population Health Model (POHEM): an overview of rationale, methods and applications. Population health metrics, 2015. 13(1): p. 24.
- Tam, J., et al., Projecting the effects of tobacco control policies in the USA through microsimulation: a study protocol. BMJ open, 2018. 8(3): p. e019169.
- Arnold, K.F., et al., DAG-informed regression modelling, agent-based modelling and microsimulation modelling: a critical comparison of methods for causal inference. International journal of epidemiology, 2018.
- Card, N.A., Lag as moderator meta-analysis: A methodological approach for synthesizing longitudinal data. International Journal of Behavioral Development, 2019. 43(1): p. 80-89.
- McCracken, J.M., Exploratory Causal Analysis in Bivariate Time Series Data http://ebot.gmu.edu/bitstream/handle/1920/10169/McCracken_gmu_0883E_11004.pdf?sequence=1&isAllowed=y. 2015.
- Hannisdal, B. and L.H. Liow, Causality from palaeontological time series. Palaeontology, 2018. 61(4): p. 495-509.
- Rupe, A. and J.P. Crutchfield, Local causal states and discrete coherent structures. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018. 28(7): p. 075312.
- Liang, X.S., Causation and information flow with respect to relative entropy. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018. 28(7): p. 075311.
- Runge, J., Causal network reconstruction from time series: From theoretical assumptions to practical estimation. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018. 28(7): p. 075310.
- Paluš, M., et al., Causality, dynamical systems and the arrow of time. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018. 28(7): p. 075307.
- Roy, S. and B. Jantzen, Detecting causality using symmetry transformations. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018. 28(7): p. 075305.
- Smirnov, D.A., Transient and equilibrium causal effects in coupled oscillators. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018. 28(7): p. 075303.
- Amigó, J.M. and Y. Hirata, Detecting directional couplings from multivariate flows by the joint distance distribution. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018. 28(7): p. 075302.
- Bollt, E.M., J. Sun, and J. Runge, Introduction to Focus Issue: Causation inference and information flow in dynamical systems: Theory and applications. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018. 28(7): p. 075201.
- Klasnja, P., et al., Microrandomized trials: An experimental design for developing just-in-time adaptive interventions. Health Psychology, 2015. 34(S): p. 1220.
- Dempsey, W., et al., The stratified micro-randomized trial design: sample size considerations for testing nested causal effects of time-varying treatments arXiv preprint arXiv:1711.03587. 2017.
- Lei, H., A. Tewari, and S.A. Murphy, An actor-critic contextual bandit algorithm for personalized mobile health interventions https://arxiv.org/pdf/1706.09090.pdf. 2017.
- Lei, H., A. Tewari, and S. Murphy, An actor-critic contextual bandit algorithm for personalized interventions using mobile devices. Advances in Neural Information Processing Systems, 2014. 27.
- Nikolakopoulos, S., I. van der Tweel, and K.C.B. Roes, Dynamic borrowing through empirical power priors that control type I error. Biometrics, 2018. 74(3): p. 874-880.
- Gravestock, I., L. Held, and O.b.o.t.C.-N. consortium, Adaptive power priors with empirical Bayes for clinical trials. Pharmaceutical Statistics, 2017. 16(5): p. 349-360.
- Banbeta, A., et al., Modified power prior with multiple historical trials for binary endpoints. Statistics in Medicine, 2019. 38(7): p. 1147-1169.
- Nagase, M., et al., Optimal designs for regional bridging studies using the Bayesian power prior method. Pharmaceutical Statistics. n/a(n/a).
- Isogawa, N., et al., A Comparison Between a Meta-analytic Approach and Power Prior Approach to Using Historical Control Information in Clinical Trials With Binary Endpoints. Therapeutic innovation & regulatory science, 2019: p. 2168479019862531.
- Ollier, A., et al., An adaptive power prior for sequential clinical trials – Application to bridging studies. Statistical Methods in Medical Research. 0(0): p. 0962280219886609.
- Wiesenfarth, M. and S. Calderazzo, Quantification of prior impact in terms of effective current sample size. Biometrics, 2019. n/a(n/a).
- Gravestock, I. and L. Held, Power priors based on multiple historical studies for binary outcomes. Biometrical Journal, 2019. 61(5): p. 1201-1218.
- Brakenhoff, T., K. Roes, and S. Nikolakopoulos, Bayesian sample size re-estimation using power priors. Statistical Methods in Medical Research, 2019. 28(6): p. 1664-1675.
- Ibrahim, J.G. and M.-H. Chen, Power prior distributions for regression models. Statistical Science, 2000. 15(1): p. 46-60.
- Wang, C., et al., Propensity score-integrated power prior approach for incorporating real-world evidence in single-arm clinical studies. Journal of Biopharmaceutical Statistics, 2019. 29(5): p. 731-748.
- Riley, K.F. and M.P. Hobson, Essential mathematical methods for the physical sciences. 2011: Cambridge University Press.
- Tsonis, A.A., et al., Convergent cross mapping: theory and an example, in Advances in Nonlinear Geosciences. 2018, Springer. p. 587-600.
- Onisko, A., Medical diagnosis, in Bayesian networks: a practical guide to applications, O. Pourret, P. Naïm, and B. Marcot, Editors. 2008, John Wiley & Sons. p. 15-32.
- Onisko, A., M.J. Druzdzel, and H. Wasyluk. Handling Incomplete Data in Learning. in Intelligent Information Systems 2002: Proceedings of the IIS’2002 Symposium, Sopot, Poland, June 3–6, 2002. 2013. Springer Science & Business Media.
- Lee, B.Y., et al., Economic Studies in Biosurveillance. Handbook of Biosurveillance, 2006: p. 423.
- Szczygieł, J., et al., Probabilistic graphical model supporting early diagnosis of autism spectrum disorder. Advances in Computer Science Research, 2014.
- Oniśko, A., Knowledge acquisition from human experts for building bayesian network models. Zeszyty Naukowe Politechniki Białostockiej. Informatyka, 2007: p. 109-119.
- Onisko, A. and R.M. Austin, Dynamic Bayesian network for cervical cancer screening, in Foundations of Biomedical Knowledge Representation. 2015, Springer. p. 207-218.
- Onisko, A., A. Tucker, and M.J. Druzdzel, Prediction and prognosis of health and disease, in Foundations of Biomedical Knowledge Representation. 2015, Springer. p. 181-188.
- Wagner, M.M., G.L. Wallstrom, and A. Onisko. Issue a boil-water advisory or wait for definitive information? a decision analysis. in AMIA Annual Symposium Proceedings. 2005. American Medical Informatics Association.
- Oniésko, A., P. Lucas, and M.J. Druzdzel. Comparison of rule-based and Bayesian network approaches in medical diagnostic systems. in Conference on Artificial Intelligence in Medicine in Europe. 2001. Springer.
- Onisko, A., M.J. Druzdzel, and R.M. Austin, How to interpret the results of medical time series data analysis: classical statistical approaches versus dynamic Bayesian network modeling. Journal of pathology informatics, 2016. 7.
- Onisko, A., M.J. Druzdzel, and R.M. Austin, Application of Bayesian network modeling to pathology informatics. Diagnostic cytopathology, 2019. 47(1): p. 41-47.
- Onisko, A. and M.J. Druzdzel, Effect of imprecision in probabilities on Bayesian network models: An empirical study. Model-based and Qualitative Reasoning in Biomedicine, 2003: p. 45.
- Austin, R.M., A. Onisko, and M.J. Druzdzel, The Pittsburgh cervical cancer screening model: a risk assessment tool. Archives of pathology & laboratory medicine, 2010. 134(5): p. 744-750.
- Druzdzel, M.J., et al. Knowledge Engineering for Very Large Decision-analytic Medical Models. in AMIA. 1999.
- Oniśko, A., M.J. Druzdzel, and H. Wasyluk, Learning Bayesian network parameters from small data sets: Application of Noisy-OR gates. International Journal of Approximate Reasoning, 2001. 27(2): p. 165-182.
- Onisko, A., M.J. Druzdzel, and H. Wasyluk. A Bayesian network model for diagnosis of liver disorders. in Proceedings of the Eleventh Conference on Biocybernetics and Biomedical Engineering. 1999. Citeseer.
- Oniśko, A., M.J. Druzdzel, and H. Wasyluk, Extension of the Hepar II model to multiple-disorder diagnosis, in Intelligent Information Systems. 2000, Springer. p. 303-313.
- Onisko, A., M.J. Druzdzel, and H. Wasyluk. A probabilistic causal model for diagnosis of liver disorders. in Proceedings of the Seventh International Symposium on Intelligent Information Systems (IIS—98). 1998.
- Kraaijeveld, P., et al. Genierate: An interactive generator of diagnostic Bayesian network models. in Proc. 16th Int. Workshop Principles Diagnosis. 2005. Citeseer.
Footnotes:
[i] Note that the games of chance were the main data exercise for many mathematicians (and many others, called ‘natural philosophers’ back in the day) who advanced the science of ‘numbers’. The classic history of statistics by Stigler [1] is a fascinating read; mentioning e.g. De Moivre’s Doctrine of Chances (1738): ‘For example, if De Moivre or someone else of his era knew that of 346 men of age fifty, only 142 survived to age seventy, 10 he might ask, “How much credence can I give to the ratio 142/346 as an estimate of the chance of surviving from fifty to seventy? What, for example, is the probability this number is below 1/2?” ‘ p. 86.